0. IntroductionPermalink

Field of View(FoV) of a camera is represented as a given size $a \times b$ of view. In the simulation, we are going to randomly generate some objects in a plane. Our goal is to find out a minimal cost path. We can assume the objects are all orthogonal rectangles. If not, to picture the objects into the FoV, it must picture the circumscribed rectangle. Base on the result, we can use SSD to infer the rectangle position.

1. SimulationPermalink

We randomly scatter some rectangles as our simulation data. The goal is to find a path to scanning all of the components. For example, a visualization of objects might looks like

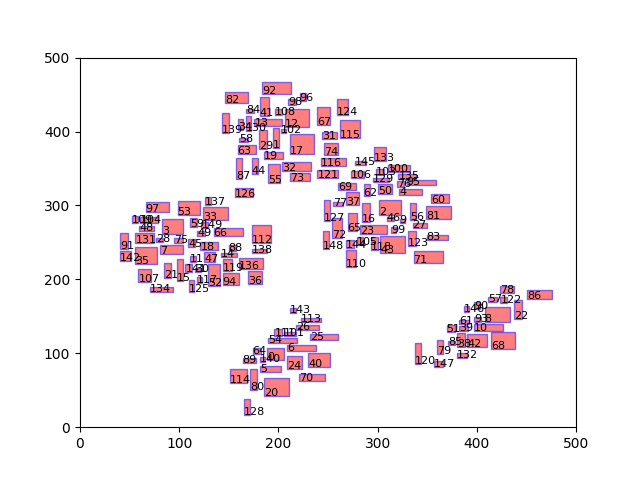
Then we demo with the following parameters:

• FoV size $100 \times 100$
• Picture cost $1$ second per frame
• Camera moving velocity $10$ unit per second

Under these setting, we are going to find our minimal time cost path planning of camera. To simplify, we assume the camera need to back to origin, then we can reduce two parameters: start and end posistions.

2. Genetic AlgorithmPermalink

This application has two cost – picturing cost and moving cost. A heuristic idea to solve the problem is clustering of the rectangles into minimal number of FoVs and regard the center of FoVs as a Travelling Salesman Problem. This approach might lead to the sub-optimal solutions. However, minimize the FoVs and Path Planning marginally might not lead to minimize the cost both jointly. This is a very common arguement even in other optimization scenario. For example, if the picturing cost is relatively cheap than the moving cost, then we have more FoVs to save our moving cost. Luckily, genetic algorithm provides a way to minimize the cost jointly through clustering and Travelling Salesman Problem. Genetic algorithm is used to improve the solution iteratively by generation. We can properly apply the crossover and mutation operator to improve the solution till converges.

2.1. EncodingPermalink

Before introducing the crossover and mutation. We need to encode a solution as the gene to apply our genetic algorithm scheme. There is one way to encode a solution. Suppose there are 10 objects labelled by $(0, 1,…, 9)$, an gene coding $$(0, 1, 3), (2, 9), (7, 8), (4, 5, 6)$$ is represented as

1. camera first visit cluster 0 contains (0, 1, 3)
2. camera second visit cluster 1 constains (2, 9)
3. camera third visit cluster 2 constains (7, 8)
4. camera visit cluster 3 constains (4, 5, 6, 7) and finally go back to the cluster 0 (form a loop) Then we can move to crossover and mutation

2.2. CrossoverPermalink

The crossover operator is an action on any different two genes. Suppose there are gene 1 and gene 2 encoded by

$$gene_{1}:(0, 1, 3), (2, 9), (7, 8), (4, 5, 6)$$ $$gene_{2}:(7, 8), (2, 4), (5, 6, 9), (0, 1, 3)$$

Randomly select a label from 0 to 9, find out the minimal cluster union such that both objects are all equal. For example, if we select label 2, then (2, 9) in $gene_{1}$ are selected. Next step we are going to find 2 and 9 in $gene_{2}$, so (2, 4) and (5, 6, 9) are select. Keep searching until both selected clusters contain each other.

$$gene_{1}:(0, 1, 3), \textbf{(2, 9)}, (7, 8), \textbf{(4, 5, 6)}$$ $$gene_{2}:(7, 8), \textbf{(2, 4)}, \textbf{(5, 6, 9)},(0, 1, 3)$$

Then exchange to selected cluster to complete the crossover.

$$gene_{1}:(0, 1, 3), \textbf{(2, 4)}, (7, 8), \textbf{(5, 6, 9)}$$ $$gene_{2}:(7, 8), \textbf{(2, 9)}, \textbf{(4, 5, 6)}, (0, 1, 3)$$

Finishing the crossover operator.

2.3. MutationPermalink

The mutation operator is an action on a gene. Suppose a gene is encoded by

$$gene:(0, 1, 3), (2, 9), (7, 8), (4, 5, 6)$$

Randomly select a cluster, removing all of the component to any other feasible cluster. For example, if we choose cluster (7, 8), and 7 can be moved to cluster 1 and 8 can be moved to cluster 3, it becomes

$$gene:(0, 1, 3), (2, 7, 9), (), (4, 5, 6, 8)$$

Finally, the gene become

$$gene:(0, 1, 3), (2, 7, 9), (4, 5, 6, 8)$$

3. ResultPermalink

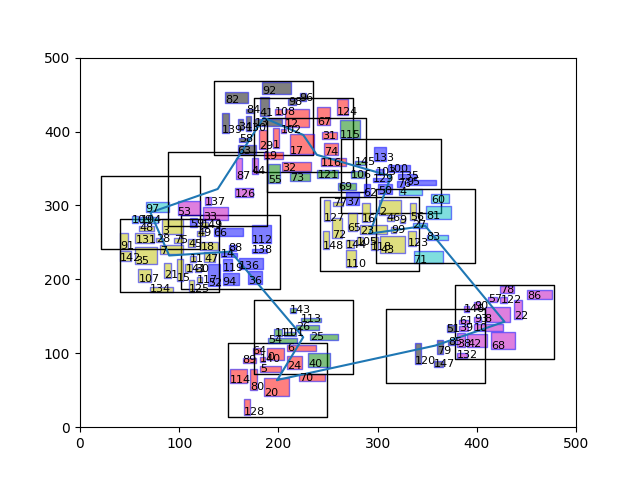
I only introduce parts of this algorithm. If you are interested in a complete guide of the algorithm, you can refer this paper. The key algorithm comes from this paper. The final path planning is

I am going to account for the optimality from these two features

1. The number of FoVs reaches minimum. There are five regions of objects aggregate. Each region we can find at least one that expand as large($100 \times 100$) as possible
2. Loop. Note in these scenario, loop without cross is a fast path to come back. Through this arguement, we believe the genetic algorithm really approach our optimal path planning.

4. SummaryPermalink

The algorithm demonstrate a realy heuristic approach of genetic algorithm. Genetic algorithm is generally applied in combinatoric optimization. The key idea is to interpret the application problem into a combinatoric problem and apply it to genetic algorithm scheme. Besides, the address the algorithm in detail, there is still a lot of geometry algorithm act on the orthogonal rectangles. This is also a very good practice of to optimize the algorithm.