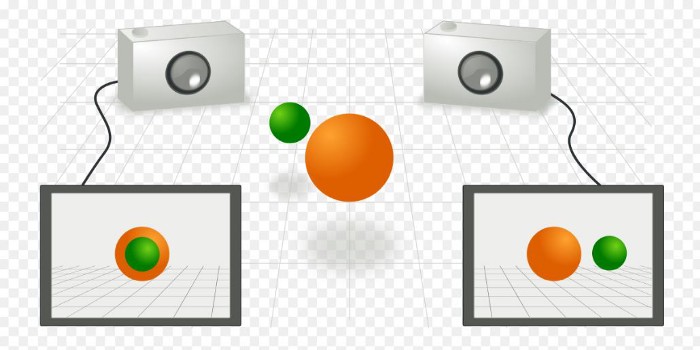
3D Contour Trajectories Reconstruction through Multiple Views

0. Simulation

First we are going to simulate the ground truth to demo this case. We simulate some 3D contours and project the contours into certain views.

# set control pts
ctrl = np.array([[-10, 10, 100], [0, 10, 120], [70, 70, 70], [100, 100, 0]])
diff = np.vstack([np.zeros(shape=(1, 3)), np.diff(ctrl, axis=0)])
t = np.linalg.norm(diff, axis=1)
t /= t[-1]

# fit
curve = np.polyfit(t1, ctrl1, deg=3)

curve is our sample contour in 3D. Then we are going to copy and add some perturbation to create different contours.

Then, we apply two camera matrices to project the contour into different view. Here we use a triangular mesh of tube to implement the projection. We project each triangular into 2D and fill with white. These are our segmentation of the projected contours.

Of course, we can picture the corresponding ground truth.

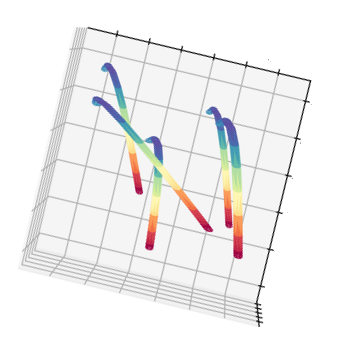
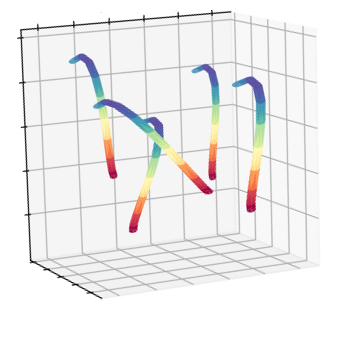
Notice that in the simulation, I intend to create a dense contours case. So the contours in 2D are usually occluded, even missing. This would lead some classical feature matching fail such like block-matching algorithm. Up to now, we have prepared all the simulation data in the algorithm.

1. Segmentation

We quickly brief this part since there are bunch of material of segmentation. The most popular way is applying segmenntation of Convolution Neural Network(CNN). This is a standard semantic segmentation problem. We collect the ground truth and label images on CNN and training. Some base networks are recommanded in this application, FCN and U-Net.

2. 3D Estimation from 2D Observation

We use the previous simulated data as example. It is necessary to provide a estimation formula. For curve fitting, the most common idea is Least Square Estimation. However, there are still three issues we can see:

1. How to apply least square from 2D to 3D?
2. How to solve overlap contour in 2D?
3. How do we estimate a general 3D contour from just unordered point set?

Since issue 3 is a general and independent topic, I would write the other post in my blog to describe it. Here we only introduce 1 and 2.

2.1. How do we apply least square from 2D to 3D?

We denote \(\gamma\) is the 3D contour and \(P\) is the \(2 \times 3\) project matrix. A notation \(P\gamma\) is the 2D contour of \(\gamma\) with respect to projection matrix \(P\). Now we can rewrite our least square approach in the form:

Suppose we observe \((P_{1}, u_{1}), (P_{2}, u_{2}), …, (P_{n}, u_{n})\) from a body of \(P_{i}\gamma\), the least square objective function is: \[ SSE(\gamma) = \sum_{i=1}^{n} \lVert P_{i}\gamma - u_{i} \rVert ^{2} \] \(\lVert P_{i}\gamma - u_{i} \rVert ^{2}\) is the minimum distance from contour \(P_{i}\gamma\) to \(u_{i}\).

Find a \(\gamma\) to minimize \(SSE\) is the least square estimator of \(\gamma\).

2.2. How to solve overlap contour

The white pixels only indicates the contour body, but do not tell us which pixel belongs to which contour. We do need to classify each pixel to the correct contour. It arise a classfication problem. Generally, if pixel \(u\) is closer to contour \(\gamma_{k}\), it is higher probability to \(\gamma_{k}\). Base on the observation, we know the contours would interact with each other. We should estimate all contours at once instead estimate contour by contour. This is one of the contribution of the project. It lead to our next approach – EM algorithm.

3. Expectation–maximization algorithm

Expectation–maximization algorithm perfectly draft our scenario. EM algorithm usually draft the checken-eggs problem. To find the contour trajectory, we need the proper classification of pixels. To find a classification of pixel. we need a proper contour trajectory to help us. EM algorithm just tell us “guess it!” and keep iterating both until it converges.

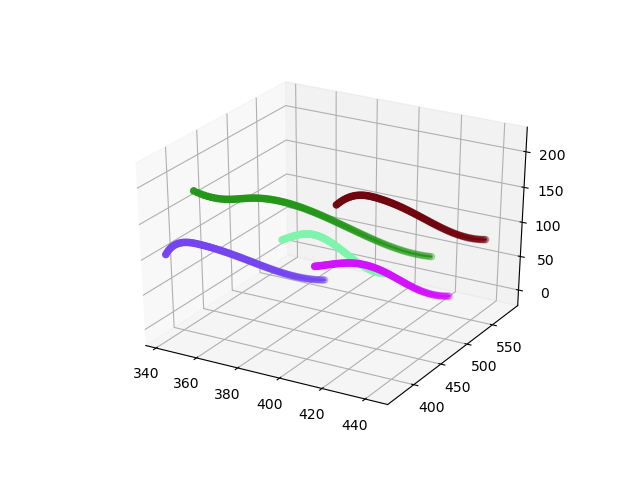
4. Result

We demostrate the 3D contours and project through the projection matrix to validate.

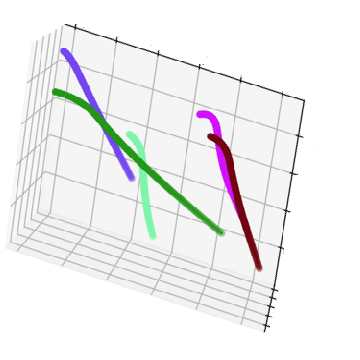
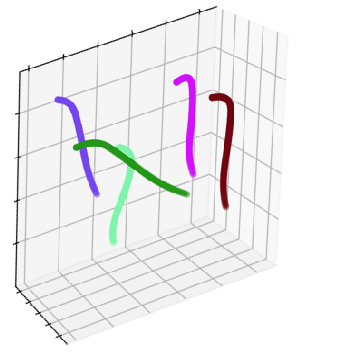
Project the 3D contour into corresponding views.

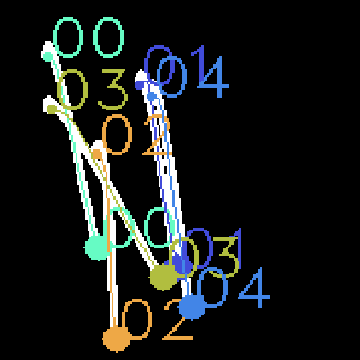
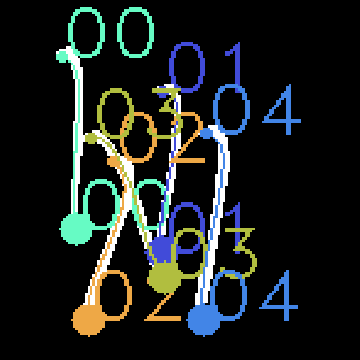
Benchmark between ground truth and result

3D reconstruction result for 2 views sample.

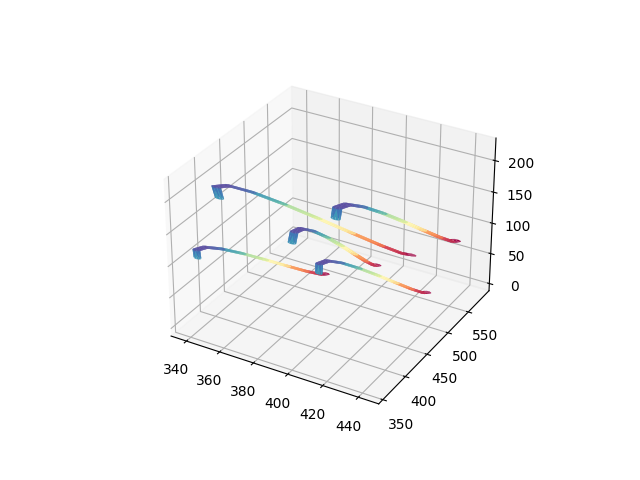
5. Summary

This is a very interesting project of 3D reconstruction problem. Traditionally, we reconstruct 3D object from 2D by some feature matching properties. However, in this project

• Object might changes fast in different views.
• Object might missing in different views.

It is hardly work when we apply the traditional strategies. Besides, I expect this workflow can have a variety of applications. It says if we can correctly describe the kernel(in this case, the kernel is contour), then we can find out the correct pattern via iterating the kernel. If you think this application is helpful to you, welcome to contact me through my e-mail.