Contour Fitting : Parametric Curve

I want to talk about a general contour fitting approach. Before introduction, I would like to clarify the difference between contour fitting and curve fitting.

Curve Fitting v.s. Contour Fitting

Curve fitting is an entry-level topic for Statistics. Generally, it is going to fit a function \(y=f(x)\) for given observation \((x_{i}, y_{i})\). Contour fitting looks similar to curve fitting but it contains more issues. Contour fitting is going to infer the parametric curve \(\gamma (t) = [x(t), y(t)]^{T}\) for given observation \((x_{i}, y_{i})\) (or sometimes, \((x_{i}, y_{i}, t_{i})\)). You might think does there have any difference in real application? Yes, it does. Look these two scenario, you will find it is necessary to develop the contour fitting to handle these problems.

Finding t

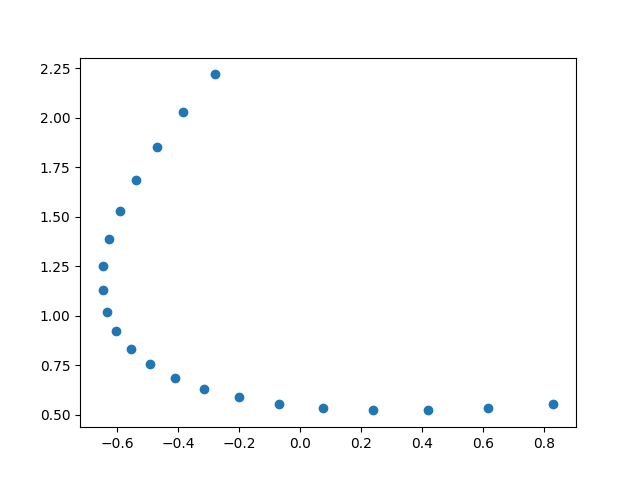
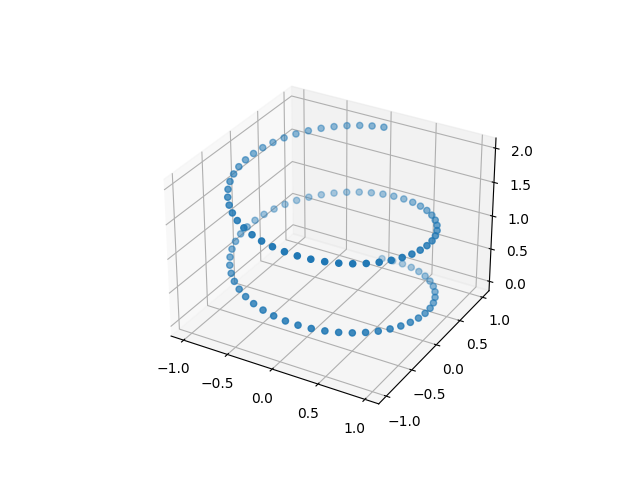
Mostly, we don’t observe the information of \(t_{i}\), so we need a convinciable idea to create \(t_{i}\). A common approach is to restrict \(t_{i}\) between (0, 1) and proportional to the arc length. We can formulate the problem as follow \[ (x_{i}, y_{i}) \textrm{ comes from } \gamma + \epsilon_{i} \textrm{ for some } t_{i} \quad i = 1,2,…,n \] Our objective is trying to apply least square estimation, which would look like \[ SSE(\gamma) = \sum_{i=1}^{n} \lVert \gamma(t_{i}) - [x_{i}, y_{i}]^{T} \rVert ^{2} \] is minimum.

However, you there is an ambiguous problem. For arbitrary point set, there might be more than one reasonable solutions. The root cause is we don’t know the order of the point set with respect to \(t\) of \(\gamma(t)\). 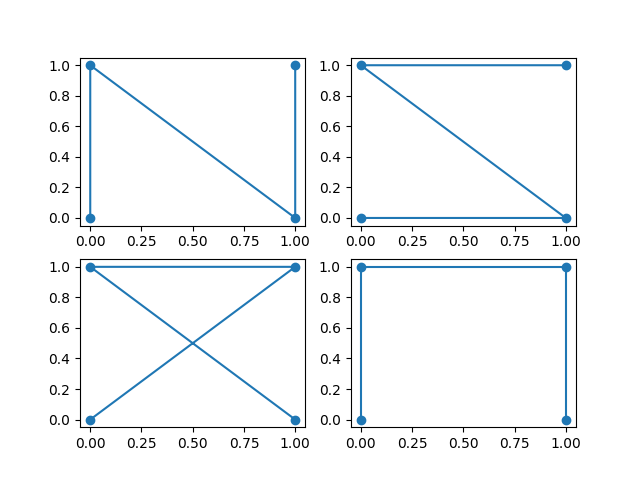There are two branches

• Order of point set is known
• Order of point set is unknown I am going to explain how to deal with it in general application. There might be variant depend on the real situation, but the principle is still applicable.

Ordered point set

Denote \(u_{i} = [x_{i}, y_{i}]^{T}\). In this case, we can use the polyline assumption to approximate \(t_{i}\). Assume \(t_{0} = 0\) \[ t_{k} = \sum_{i=1}^{n} \lVert u_{i} - u_{i-1} \rVert \] This make \(t_{k}\) approximate to the arc length in first order. To restrict \(t_{k}\) locate in \((0, 1)\), apply \[ t_{k} = t_{k} / t_{-1} \quad \textrm{ for all } k=1,2,…,n \] \[ \textrm{where } t_{-1} \textrm{ refers to the last term of } t_{k} \]

Unordered point set

If we just observe the points without ordering, one way is try to find out the order of the points. One straightforward approach is to find the shortest path passing throught all points. However, finding shortest path is a NP-complete problem. It usually fails when the observation is large. We need a more trustworthy solution. In next article, I will provide an iterative solution call projection index, which show a deep understanding of the parameter \(t\).

• 2020 3